Умозаключение – это форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением (выводом). Например:

Все живые организмы питаются влагой.

Все растения – это живые организмы.

=> Все растения питаются влагой.

В приведенном примере первые два суждения являются посылками, а третье – выводом. Посылки должны быть истинными суждениями и должны быть связаны между собой. Если хотя бы одна из посылок ложна, то и вывод ложен:

Все птицы – это млекопитающие животные.

Все воробьи – это птицы.

=> Все воробьи – это млекопитающие животные.

Как видим, в приведенном примере ложность первой посылки приводит к ложному выводу, несмотря на то что вторая посылка является истинной. Если посылки между собой не связаны, то вывод из них сделать невозможно. Например, из следующих двух посылок никакого вывода не следует:

Все планеты – это небесные тела.

Все сосны являются деревьями.

=>?

Обратим внимание на то, что умозаключения состоят из суждений, а суждения – из понятий, т. е. одна форма мышления входит в другую в качестве составной части.

Все умозаключения делятся на непосредственные и опосредованные.

В непосредственных умозаключениях вывод делается из одной посылки. Например:

Все цветы являются растениями.

=> Некоторые растения являются цветами.

Верно, что все цветы являются растениями.

=> Неверно, что некоторые цветы не являются растениями.

Нетрудно догадаться, что непосредственные умозаключения представляют собой уже известные нам операции преобразования простых суждений и выводы об истинности простых суждений по логическому квадрату. Первый приведенный пример непосредственного умозаключения является преобразованием простого суждения путем обращения, а во втором примере по логическому квадрату из истинности суждения вида А делается вывод о ложности суждения вида О.

В опосредованных умозаключениях вывод делается из нескольких посылок. Например:

Все рыбы – это живые существа.

Все караси – это рыбы.

=> Все караси – это живые существа.

Опосредованные умозаключения делятся на три вида: дедуктивные, индуктивные и умозаключения по аналогии.

Дедуктивные умозаключения (дедукция) (от лат. deductio – «выведение») – это умозаключения, в которых из общего правила делается вывод для частного случая (из общего правила выводится частный случай). Например:

Все звезды излучают энергию.

Солнце – это звезда.

=> Солнце излучает энергию.

Как видим, первая посылка представляет собой общее правило, из которого (при помощи второй посылки) вытекает частный случай в виде вывода: если все звезды излучают энергию, значит, Солнце тоже ее излучает, потому что оно является звездой.

В дедукции рассуждение идет от общего к частному, от большего к меньшему, знание сужается, в силу чего дедуктивные выводы достоверны, т. е. точны, обязательны, необходимы. Посмотрим еще раз на приведенный пример. Мог бы из двух данных посылок вытекать иной вывод, кроме того, который из них вытекает? Не мог. Вытекающий вывод – единственно возможный в этом случае. Изобразим отношения между понятиями, из которых состояло наше умозаключение, кругами Эйлера. Объемы трех понятий: звезды (3); тела, излучающие энергию (Т) и Солнце (С) схематично расположатся следующим образом (рис. 33).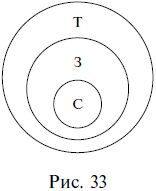

Если объем понятия звезды включается в объем понятия тела, излучающие энергию, а объем понятия Солнце включается в объем понятия звезды, то объем понятия Солнце автоматически включается в объем понятия тела, излучающие энергию, в силу чего дедуктивный вывод и является достоверным.

Несомненное достоинство дедукции заключается в достоверности ее выводов. Вспомним, известный литературный герой Шерлок Холмс пользовался дедуктивным методом при раскрытии преступлений. Это значит, что он строил свои рассуждения таким образом, чтобы из общего выводить частное. В одном произведении, объясняя доктору Ватсону сущность своего дедуктивного метода, он приводит такой пример. Около убитого полковника Эшби сыщики Скотланд-Ярда обнаружили выкуренную сигару и решили, что полковник выкурил ее перед смертью. Однако Шерлок Холмс неопровержимо доказывает, что полковник не мог выкурить эту сигару, потому что он носил большие, пышные усы, а сигара выкурена до конца, т. е., если бы ее курил полковник Эшби, то он непременно подпалил бы свои усы. Следовательно, сигару выкурил другой человек.

В этом рассуждении вывод выглядит убедительно именно потому, что он дедуктивный – из общего правила: Любой человек с большими, пышными усами не может выкурить сигару до конца, выводится частный случай: Полковник Эшби не мог выкурить сигару до конца, потому что носил такие усы. Приведем рассмотренное рассуждение к принятой в логике стандартной форме записи умозаключений в виде посылок и вывода:

Любой человек с большими, пышными усами не может выкурить сигару до конца.

Полковник Эшби носил большие, пышные усы.

=> Полковник Эшби не мог выкурить сигару до конца.

Индуктивные умозаключения (индукция) (от лат. inductio – «наведение») – это умозаключения, в которых из нескольких частных случаев выводится общее правило. Например:

Юпитер движется.

Марс движется.

Венера движется.

Юпитер, Марс, Венера – это планеты.

=> Все планеты движутся.

Первые три посылки представляют собой частные случаи, четвертая посылка подводит их под один класс объектов, объединяет их, а в выводе говорится обо всех объектах этого класса, т. е. формулируется некое общее правило (вытекающее из трех частных случаев).

Легко увидеть, что индуктивные умозаключения строятся по принципу, противоположному построению дедуктивных умозаключений. В индукции рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы (в отличие от дедуктивных) не достоверны, а вероятностны. В рассмотренном выше примере индукции признак, обнаруженный у некоторых объектов какой-то группы, перенесен на все объекты этой группы, сделано обобщение, которое почти всегда чревато ошибкой: вполне возможно наличие в группе каких-то исключений, и даже если множество объектов из некоторой группы характеризуется каким-то признаком, то это не означает, что таким признаком характеризуются все объекты данной группы. Вероятностный характер выводов является, конечно же, недостатком индукции. Однако ее несомненное достоинство и выгодное отличие от дедукции, которая представляет собой сужающееся знание, заключается в том, что индукция – это расширяющееся знание, способное приводить к новому, в то время как дедукция – это разбор старого и уже известного.

Умозаключения по аналогии (аналогия) (от греч. analogia – «соответствие») – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь.

Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода.

=> Вероятно, на Марсе есть жизнь.

Как видим, сопоставляются два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в Солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.

Все дедуктивные умозаключения называются силлогизмами (от греч. sillogismos – «подсчитывание, подытоживание, выведение следствия»). Существует несколько видов силлогизмов. Первый из них называется простым, или категорическим, потому что все входящие в него суждения (две посылки и вывод) являются простыми, или категорическими. Это уже известные нам суждения видов А, I, Е, О.

Рассмотрим пример простого силлогизма:

Все цветы (М) – это растения (Р).

Все розы (S) – это цветы (М).

=> Все розы (S) – это растения (Р).

Обе посылки и вывод являются в данном силлогизме простыми суждениями, причем и посылки, и вывод – это суждения вида А (общеутвердительные). Обратим внимание на вывод, представленный суждением Все розы – это растения. В этом выводе субъектом выступает термин розы, а предикатом – термин растения. Субъект вывода присутствует во второй посылке силлогизма, а предикат вывода – в первой. Так же в обеих посылках повторяется термин цветы, который, как нетрудно увидеть, является связующим: именно благодаря ему не связанные, разобщенные в посылках термины растения и розы можно связать в выводе. Таким образом, структура силлогизма включает в себя две посылки и один вывод, которые состоят из трех (различным образом расположенных) терминов.

Субъект вывода располагается во второй посылке силлогизма и называется меньшим термином силлогизма (вторая посылка также называется меньшей).

Предикат вывода располагается в первой посылке силлогизма и называется б?ольшим термином силлогизма (первая посылка также называется большей). Предикат вывода, как правило, является по объему большим понятием, чем субъект вывода (в приведенном примере понятия розы и растения находятся в отношении родовидового подчинения), в силу чего предикат вывода называется б?ольшим термином, а субъект вывода – меньшим.

Термин, который повторяется в двух посылках и связывает субъект с предикатом (меньший и больший термины), называется средним термином силлогизма и обозначается латинской буквой М (от лат. medium – «средний»).

Три термина силлогизма могут быть расположены в нем по-разному. Взаимное расположение терминов друг относительно друга называется фигурой простого силлогизма. Таких фигур четыре, т. е. все возможные варианты взаимного расположения терминов в силлогизме исчерпываются четырьмя комбинациями. Рассмотрим их.

Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином. Например:

Все газы (М) – это химические элементы (Р).

Гелий (S) – это газ (М).

=> Гелий (S) – это химический элемент (Р).

Учитывая, что в первой посылке средний термин связан с предикатом, во второй посылке субъект связан со средним термином, а в выводе субъект связан с предикатом, составим схему расположения и связи терминов в приведенном примере (рис. 34).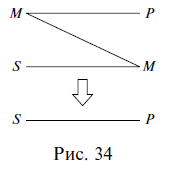

Прямые линии на схеме (за исключением той, которая отделяет посылки от вывода) показывают связь терминов в посылках и в выводе. Поскольку роль среднего термина заключается в том, чтобы связывать больший и меньший термины силлогизма, то на схеме средний термин в первой посылке соединяется линией со средним термином во второй посылке. Схема показывает, каким именно образом средний термин связывает между собой другие термины силлогизма в его первой фигуре. Кроме того, отношения между тремя терминами можно изобразить с помощью кругов Эйлера. В данном случае получится следующая схема (рис. 35).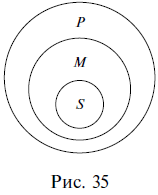

Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином. Например:

Все рыбы (Р) дышат жабрами (М).

Все киты (S) не дышат жабрами (М).

=> Все киты (S) не рыбы (Р).

Схемы взаимного расположения терминов и отношений между ними во второй фигуре силлогизма выглядят так, как показано на рис. 36.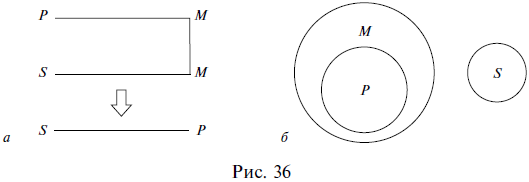

Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

Все тигры (М) – это млекопитающие (Р).

Все тигры (М) – это хищники (S).

=> Некоторые хищники (S) – это млекопитающие (Р).

Схемы взаимного расположения терминов и отношений между ними в третьей фигуре силлогизма изображены на рис. 37.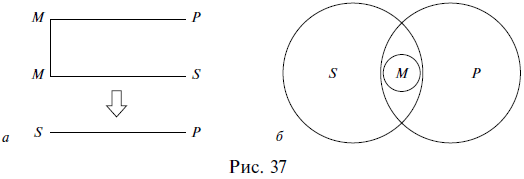

Четвертая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него. Например:

Все квадраты (Р) – это прямоугольники (М).

Все прямоугольники (М) – это не треугольники (S).

=> Все треугольники (S) – это не квадраты (Р).

Схемы взаимного расположения терминов и отношений между ними в четвертой фигуре силлогизма показаны на рис. 38.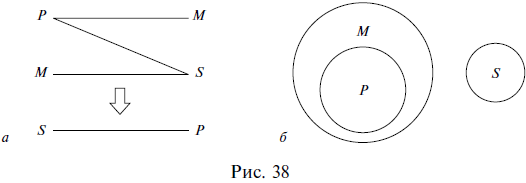

Отметим, что отношения между терминами силлогизма во всех фигурах могут быть и другими.

Любой простой силлогизм состоит из трех суждений (двух посылок и вывода). Каждое из них является простым и принадлежит к одному из четырех видов (А, I, Е, О). Набор простых суждений, входящих в силлогизм, называется модусом простого силлогизма. Например:

Все небесные тела движутся.

Все планеты – это небесные тела.

=> Все планеты движутся.

В этом силлогизме первая посылка является простым суждением вида А (общеутвердительным), вторая посылка – это тоже простое суждение вида А, и вывод в данном случае представляет собой простое суждение вида А. Поэтому рассмотренный силлогизм имеет модус AAA, или barbara. Последнее латинское слово ничего не обозначает и никак не переводится – это просто сочетание букв, подобранное таким образом, чтобы в нем присутствовали три буквы а, символизируя собой модус силлогизма AAA. Латинские «слова» для обозначения модусов простого силлогизма были придуманы еще в Средние века.

Следующий пример – силлогизм с модусом ЕАЕ, или cesare:

Все журналы – это периодические издания.

Все книги не являются периодическими изданиями.

=> Все книги не являются журналами.

И еще один пример. Этот силлогизм имеет модус AAI, или darapti.

Все углероды – простые тела.

Все углероды электропроводны.

=> Некоторые электропроводники – простые тела.

Всего модусов во всех четырех фигурах (т. е. возможных комбинаций простых суждений в силлогизме) – 256. В каждой фигуре 64 модуса. Однако из этих 256 модусов только 19 дают достоверные выводы, остальные приводят к вероятностным выводам. Если принять во внимание, что одним из главных признаков дедукции (а значит, и силлогизма) является достоверность ее выводов, то становится понятным, почему эти 19 модусов называются правильными, а остальные – неправильными.

Наша задача – уметь определять фигуру и модус любого простого силлогизма. Например, требуется установить фигуру и модус силлогизма:

Все вещества состоят из атомов.

Все жидкости – это вещества.

=> Все жидкости состоят из атомов.

Прежде всего надо найти субъект и предикат вывода, т. е. меньший и больший термины силлогизма. Далее следует установить местоположение меньшего термина во второй посылке и большего – в первой. После этого можно определить средний термин и схематично изобразить расположение всех терминов в силлогизме (рис. 39).

Все вещества (М) состоят из атомов (Р).

Все жидкости (S) – это вещества (М).

=> Все жидкости (S) состоят из атомов (Р).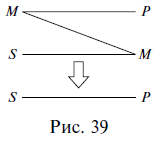

Как видим, рассматриваемый силлогизм построен по первой фигуре. Теперь надо найти его модус. Для этого следует выяснить, к какому виду простых суждений относятся первая и вторая посылки и вывод. В нашем примере обе посылки и вывод являются суждениями вида А (общеутвердительными), т. е. модус данного силлогизма – AAA, или barbara. Итак, предложенный силлогизм имеет первую фигуру и модус AAA.

Правила силлогизма делятся на общие и частные.

Общие правила применимы ко всем простым силлогизмам, независимо от того, по какой фигуре они построены. Частные правила действуют только для каждой фигуры силлогизма и поэтому часто называются правилами фигур. Рассмотрим общие правила силлогизма.

В силлогизме должно быть только три термина. Обратимся к уже упоминавшемуся силлогизму, в котором данное правило нарушено.

Движение вечно.

Хождение в школу – это движение.

=> Хождение в школу вечно.

Обе посылки этого силлогизма являются истинными суждениями, однако из них вытекает ложный вывод, потому что нарушено рассматриваемое правило. Слово движение употребляется в двух посылках в двух разных значениях: движение как всеобщее мировое изменение и движение как механическое перемещение тела из точки в точку. Получается, что терминов в силлогизме три: движение, хождение в школу, вечность, а смыслов (поскольку один из терминов употребляется в двух разных смыслах) четыре, т. е. лишний смысл как бы подразумевает лишний термин. Иначе говоря, в приведенном примере силлогизма было не три, а четыре (по смыслу) термина. Ошибка, возникающая при нарушении вышеприведенного правила, называется учетверением терминов.

Средний термин должен быть распределен хотя бы в одной из посылок. О распределенности терминов в простых суждениях речь шла в предыдущей главе. Напомним, что проще всего устанавливать распределенность терминов в простых суждениях с помощью круговых схем: надо изобразить кругами Эйлера отношения между терминами суждения, при этом полный круг на схеме будет обозначать распределенный термин (+), а неполный – нераспределенный (—). Рассмотрим пример силлогизма.

Все кошки (К) – это живые существа (Ж. с).

Сократ (С) – это тоже живое существо.

=> Сократ – это кошка.

Из двух истинных посылок вытекает ложный вывод. Изобразим кругами Эйлера отношения между терминами в посылках силлогизма и установим распределенность этих терминов (рис. 40).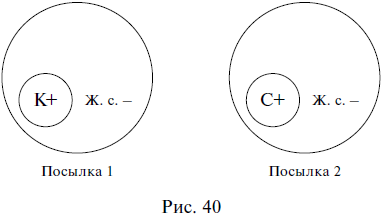

Как видим, средний термин (живые существа) в данном случае не распределен ни в одной из посылок, а по правилу он должен быть распределен хотя бы в одной. Ошибка, возникающая при нарушении рассматриваемого правила, так и называется – нераспределенность среднего термина в каждой посылке.

Термин, который был не распределен в посылке, не может быть распределен в выводе. Обратимся к следующему примеру:

Все яблоки (Я) – съедобные предметы (С. п.).

Все груши (Г) – это не яблоки.

=> Все груши – несъедобные предметы.

Посылки силлогизма являются истинными суждениями, а вывод – ложным. Как и в предыдущем случае, изобразим кругами Эйлера отношения между терминами в посылках и в выводе силлогизма и установим распределенность этих терминов (рис. 41).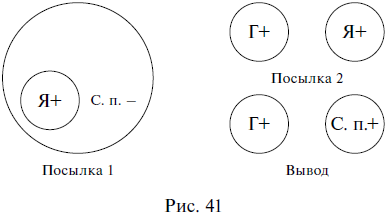

В данном случае предикат вывода, или больший термин силлогизма (съедобные предметы), в первой посылке является нераспределенным (—), а в выводе – распределенным (+), что запрещается рассматриваемым правилом. Ошибка, возникающая при его нарушении, называется расширением большего термина. Вспомним, что термин распределен, когда речь идет обо всех предметах, входящих в него, и нераспределен, когда речь идет о части предметов, входящих в него, именно поэтому ошибка и называется расширением термина.

В силлогизме не должно быть двух отрицательных посылок. Хотя бы одна из посылок силлогизма должна быть положительной (могут быть положительными и обе посылки). Если две посылки в силлогизме отрицательные, то вывод из них или вообще сделать нельзя, или же, если его сделать возможно, он будет ложным или, по крайней мере, недостоверным, вероятностным. Например:

Снайперы не могут иметь плохое зрение.

Все мои друзья – не снайперы.

=> Все мои друзья имеют плохое зрение.

Обе посылки в силлогизме являются отрицательными суждениями, и, несмотря на их истинность, из них вытекает ложный вывод. Ошибка, которая возникает в данном случае, так и называется – две отрицательные посылки.

В силлогизме не должно быть двух частных посылок.

Хотя бы одна из посылок должна быть общей (могут быть общими и обе посылки). Если две посылки в силлогизме представляют собой частные суждения, то вывод из них сделать невозможно. Например:

Некоторые школьники – это первоклассники.

Некоторые школьники – это десятиклассники.

=>?

Из этих посылок никакой вывод не следует, потому что обе они являются частными. Ошибка, возникающая при нарушении данного правила, так и называется – две частные посылки.

Если одна из посылок отрицательная, то и вывод должен быть отрицательным. Например:

Ни один металл не является изолятором.

Медь – это металл.

=> Медь не является изолятором.

Как видим, из двух посылок данного силлогизма не может вытекать утвердительный вывод. Он может быть только отрицательным.

Если одна из посылок частная, то и вывод должен быть частным. Например:

Все углеводороды – это органические соединения.

Некоторые вещества – это углеводороды.

=> Некоторые вещества – это органические соединения.

В этом силлогизме из двух посылок не может следовать общий вывод. Он может быть только частным, так как вторая посылка является частной.

Приведем еще несколько примеров простого силлогизма – как правильных, так и с нарушениями каких-то общих правил.

Все травоядные питаются растительной пищей.

Все тигры не питаются растительной пищей.

=> Все тигры не являются травоядными.

(Правильный силлогизм)

Все отличники не получают двоек.

Мой друг – не отличник.

=> Мой друг получает двойки.

(Ошибка – две отрицательные посылки в силлогизме)

Все рыбы плавают.

Все киты тоже плавают.

=> Все киты являются рыбами.

(Ошибка – средний термин не распределен ни в одной из посылок)

Лук – это древнее орудие для стрельбы.

Одна из овощных культур – это лук.

=> Одна из овощных культур – это древнее орудие для стрельбы.

(Ошибка – учетверение терминов в простом силлогизме)

Любой металл не является изолятором.

Вода – это не металл.

=> Вода является изолятором.

(Ошибка – две отрицательные посылки в силлогизме)

Ни одно насекомое не является птицей.

Все пчелы – это насекомые.

=> Ни одна пчела не является птицей.

(Правильный силлогизм)

Все стулья – это предметы мебели.

Все шкафы – это не стулья.

=> Все шкафы – это не предметы мебели.

(Ошибка – расширение большего термина в силлогизме)

Законы придумывают люди.

Всемирное тяготение – это закон.

=> Всемирное тяготение придумали люди.

(Ошибка – учетверение терминов в простом силлогизме)

Все люди смертны.

Все животные – не люди.

=> Животные бессмертны.

(Ошибка – расширение большего термина в силлогизме)

Все олимпийские чемпионы являются спортсменами.

Некоторые россияне – это олимпийские чемпионы.

=> Некоторые россияне – это спортсмены.

(Правильный силлогизм)

Материя несотворима и неуничтожима.

Шелк – это материя.

=> Шелк несотворим и неуничтожим.

(Ошибка – учетверение терминов в простом силлогизме)

Все выпускники школы сдают экзамены.

Все студенты-пятикурсники не являются выпускниками школы.

=> Все студенты-пятикурсники не сдают экзамены.

(Ошибка – расширение большего термина в силлогизме)

Все звезды не являются планетами.

Все астероиды – это малые планеты.

=> Все астероиды – не звезды.

(Правильный силлогизм)

Все дедушки являются отцами.

Все отцы – это мужчины.

=> Некоторые мужчины – это дедушки.

(Правильный силлогизм)

Ни один первоклассник не является совершеннолетним.

Все взрослые люди – это не первоклассники.

=> Все взрослые люди – это несовершеннолетние.

(Ошибка – две отрицательные посылки в силлогизме)

Простой силлогизм – это одна из широко распространенных разновидностей умозаключения. Поэтому он часто используется в повседневном и научном мышлении. Однако при его употреблении мы, как правило, не соблюдаем его четкую логическую структуру. Например:

Все рыбы не являются млекопитающими.

Все киты являются млекопитающими.

=> Следовательно, все киты не являются рыбами.

Вместо этого, мы, скорее всего, скажем: Все киты не рыбы, так как они – млекопитающие или: Все киты не рыбы, потому что рыбы – не млекопитающие. Нетрудно увидеть, что эти два умозаключения представляют собой сокращенную форму приведенного простого силлогизма.

Таким образом, в мышлении и речи обычно используется не простой силлогизм, а его различные сокращенные разновидности. Рассмотрим их.

Энтимема – это простой силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из любого силлогизма можно вывести три энтимемы. Для примера возьмем следующий силлогизм:

Все металлы электропроводны.

Железо – это металл.

=> Железо электропроводно.

Из данного силлогизма следуют три энтимемы: Железо электропроводно, так как оно является металлом (пропущена большая посылка); Железо электропроводно, потому что все металлы электропроводны (пропущена меньшая посылка); Все металлы электропроводны, а железо – это металл (пропущен вывод).

Эпихейрема – это простой силлогизм, в котором обе посылки являются энтимемами. Возьмем два силлогизма и выведем из них энтимемы.

Силлогизм 1

Все, что приводит общество к бедствиям, есть зло.

Социальная несправедливость приводит общество к бедствиям.

=> Социальная несправедливость – это зло.

Пропуская в этом силлогизме большую посылку, получаем следующую энтимему: Социальная несправедливость – это зло, так как она приводит общество к бедствиям.

Силлогизм 2

Все, что способствует обогащению одних за счет обнищания других, – это социальная несправедливость.

Частная собственность способствует обогащению одних за счет обнищания других.

=> Частная собственность – это социальная несправедливость.

Пропуская в этом силлогизме большую посылку получаем такую энтимему: Частная собственность – это социальная несправедливость, так как она способствует обогащению одних за счет обнищания других. Если расположить эти две энтимемы друг за другом, то они станут посылками нового, третьего силлогизма, который и будет эпихейремой:

Социальная несправедливость – это зло, так как оно приводит общество к бедствиям.

Частная собственность – это социальная несправедливость, так как она способствует обогащению одних за счет обнищания других.

=> Частная собственность – это зло.

Как видим, в составе эпихейремы можно выделить три силлогизма: два из них являются посылочными, а один строится из выводов посылочных силлогизмов. Этот последний силлогизм представляет собой основу для окончательного вывода.

Полисиллогизм (сложный силлогизм) – это два или несколько простых силлогизмов, связанных между собой таким образом, что вывод одного из них является посылкой следующего. Например:

Здесь и далее скобками показаны два силлогизма, объединенные в полисиллогизм.

Обратим внимание на то, что вывод предыдущего силлогизма стал большей посылкой последующего. В этом случае получившийся полисиллогизм называется прогрессивным. Если же вывод предыдущего силлогизма становится меньшей посылкой последующего, то полисиллогизм называется регрессивным. Например:

Вывод предыдущего силлогизма является меньшей посылкой следующего. Можно заметить, что в этом случае два силлогизма невозможно графически соединить в последовательную цепочку, как в случае прогрессивного полисиллогизма.

Выше говорилось, что полисиллогизм может состоять не только из двух, но и из большего числа простых силлогизмов. Приведем пример полисиллогизма (прогрессивного), который состоит из трех простых силлогизмов:

Сорит (сложносокращенный силлогизм) – это полисиллогизм, в котором пропущена посылка последующего силлогизма, являющаяся выводом предыдущего. Вернемся к рассмотренному выше примеру прогрессивного полисиллогизма и пропустим в нем большую посылку второго силлогизма, которая представляет собой вывод первого силлогизма. Получится прогрессивный сорит:

Все, что развивает мышление, полезно.

Все интеллектуальные игры развивают мышление.

Шахматы – это интеллектуальная игра.

=> Шахматы полезны.

Теперь обратимся к рассмотренному выше примеру регрессивного полисиллогизма и пропустим в нем меньшую посылку второго силлогизма, которая является выводом первого силлогизма. Получится регрессивный сорит:

Все звезды – это небесные тела.

Солнце – это звезда.

Все небесные тела участвуют в гравитационных взаимодействиях.

=> Солнце участвует в гравитационных взаимодействиях.

Умозаключения, которые содержат в себе разделительные (дизъюнктивные) суждения, называются разделительными. В мышлении и речи часто используется разделительно-категорический силлогизм, в котором, как явствует из названия, первая посылка представляет собой разделительное (дизъюнктивное) суждение, а вторая посылка – простое (категорическое) суждение. Например:

Учебное заведение может быть начальным, или средним, или высшим.

МГУ является высшим учебным заведением.

=> МГУ – это не начальное и не среднее учебное заведение.

Разделительно-категорический силлогизм имеет два модуса: утверждающе-отрицающий и отрицающе-утверждающий.

В утверждающе-отрицающем модусе первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, вторая утверждает один из них, а вывод отрицает все остальные (таким образом, рассуждение движется от утверждения к отрицанию). Например:

Леса бывают хвойными, или лиственными, или смешанными.

Этот лес хвойный.

=> Этот лес не лиственный и не смешанный.

В отрицающе-утверждающем модусе первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, вторая отрицает все данные варианты, кроме одного, а вывод утверждает один оставшийся вариант (таким образом, рассуждение движется от отрицания к утверждению). Например:

Люди бывают европеоидами, или монголоидами, или негроидами.

Этот человек не монголоид и не негроид.

=> Этот человек является европеоидом.

Первая посылка разделительно-категорического силлогизма является строгой дизъюнкцией, т. е. представляет собой уже знакомую нам логическую операцию деления понятия. Поэтому неудивительно, что правила этого силлогизма повторяют известные нам правила деления понятия. Рассмотрим их.

Деление в первой посылке должно проводиться по одному основанию. Например:

Транспорт бывает наземным, или подземным, или водным, или воздушным, или общественным.

Пригородные электропоезда – это общественный транспорт.

=> Пригородные электропоезда – это не наземный, не подземный, не водный и не воздушный транспорт.

Силлогизм построен по утверждающе-отрицающему модусу: в первой посылке представлено несколько вариантов, во второй посылке один из них утверждается, в силу чего в выводе отрицаются все остальные. Однако из двух истинных посылок вытекает ложный вывод.

Почему так получается? Потому что в первой посылке деление проводилось по двум разным основаниям: в какой природной среде передвигается транспорт и кому он принадлежит. Уже знакомая нам подмена основания деления в первой посылке разделительно-категорического силлогизма приводит к ложному выводу.

Деление в первой посылке должно быть полным. Например:

Математические действия бывают сложением, или вычитанием, или умножением, или делением.

Логарифмирование – это не сложение, не вычитание, не умножение и не деление.

=> Логарифмирование – это не математическое действие.

Известная нам ошибка неполного деления в первой посылке силлогизма обусловливает ложный вывод, вытекающий из истинных посылок.

Результаты деления в первой посылке не должны пересекаться, или дизъюнкция должна быть строгой. Например:

Страны мира бывают северными, или южными, или западными, или восточными.

Канада – это северная страна.

=> Канада – это не южная, не западная и не восточная страна.

В силлогизме вывод является ложным, так как Канада в такой же степени северная страна, в какой и западная. Ложный вывод при истинных посылках объясняется в данном случае пересечением результатов деления в первой посылке, или, что одно и то же, – нестрогой дизъюнкцией. Следует отметить, что нестрогая дизъюнкция в разделительно-категорическом силлогизме допустима в том случае, когда он построен по отрицающе-утверждающему модусу. Например:

Он силен от природы или же постоянно занимается спортом.

Он не является сильным от природы.

=> Он постоянно занимается спортом.

В силлогизме нет ошибки, несмотря на то что дизъюнкция в первой посылке была нестрогой. Таким образом, рассматриваемое правило безоговорочно действует только для утверждающе-отрицающего модуса разделительно-категорического силлогизма.

Деление в первой посылке должно быть последовательным. Например:

Предложения бывают простыми, или сложными, или сложносочиненными.

Это предложение сложносочиненное.

=> Это предложение не простое и не сложное.

В силлогизме ложный вывод следует из истинных посылок по той причине, что в первой посылке была допущена уже известная нам ошибка, которая называется скачком в делении.

Приведем еще несколько примеров разделительно-категорического силлогизма – как правильных, так и с нарушениями рассмотренных правил.

Четырехугольники бывают квадратами, или ромбами, или трапециями.

Эта фигура – не ромб и не трапеция.

=> Эта фигура – квадрат.

(Ошибка – неполное деление)

Отбор в живой природе бывает искусственным или естественным.

Данный отбор не является искусственным.

=> Данный отбор является естественным.

(Правильное умозаключение)

Люди бывают талантливыми, или бесталанными, или упрямыми.

Он является упрямым человеком.

=> Он не талантлив и не бесталанен.

(Ошибка – подмена основания в делении)

Учебные заведения бывают начальными, или средними, или высшими, или университетами.

МГУ – это университет.

=> МГУ – это не начальное, не среднее и не высшее учебное заведение.

(Ошибка – скачок в делении)

Можно изучать естественные науки или гуманитарные.

Я изучаю естественные науки.

=> Я не изучаю гуманитарные науки.

(Ошибка – пересечение результатов деления, или нестрогая дизъюнкция)

Элементарные частицы имеют отрицательный электрический заряд, или положительный, или нейтральный.

Электроны имеют отрицательный электрический заряд.

=> Электроны не имеют ни положительного, ни нейтрального электрического заряда.

(Правильное умозаключение)

Издания бывают периодическими, или непериодическими, или зарубежными.

Это издание является зарубежным.

=> Это издание не является периодическим и не является непериодическим.

(Ошибка – подмена основания)

Разделительно-категорический силлогизм в логике часто называют просто разделительно-категорическим умозаключением. Помимо него существует также чисто разделительный силлогизм (чисто разделительное умозаключение), обе посылки и вывод которого являются разделительными (дизъюнктивными) суждениями. Например:

Зеркала бывают плоскими или сферическими.

Сферические зеркала бывают вогнутыми или выпуклыми.

=> Зеркала бывают плоскими, или вогнутыми, или выпуклыми.

Умозаключения, которые содержат в себе условные (импликативные) суждения, называются условными. В мышлении и речи часто используется условно-категорический силлогизм, название которого свидетельствует о том, что в нем первая посылка является условным (импликативным) суждением, а вторая посылка – простым (категорическим). Например:

Если взлетная полоса покрыта льдом, то самолеты не могут взлететь.

Сегодня взлетная полоса покрыта льдом.

=> Сегодня самолеты не могут взлететь.

Условно-категорический силлогизм имеет два модуса: утверждающий и отрицающий.

Утверждающий модус – у которого первая посылка представляет собой импликацию (состоящую, как мы уже знаем, из двух частей – основания и следствия), вторая посылка является утверждением основания, а в выводе утверждается следствие. Например:

Если вещество – металл, то оно электропроводно.

Данное вещество – это металл.

=> Данное вещество электропроводно.

Отрицающий модус – у которого первая посылка представляет собой импликацию основания и следствия, вторая посылка является отрицанием следствия, а в выводе отрицается основание. Например:

Если вещество – металл, то оно электропроводно.

Данное вещество неэлектропроводно.

=> Данное вещество – не металл.

Необходимо обратить внимание на уже известную нам особенность импликативного суждения, которая состоит в том, что основание и следствие нельзя поменять местами. Например, высказывание Если вещество – металл, то оно электропроводно является верным, так как все металлы – это электропроводники (из того, что вещество – металл, с необходимостью вытекает его электропроводность). Однако высказывание Если вещество электропроводно, то оно – металл неверно, так как не все электропроводники являются металлами (из того, что вещество электропроводно, не следует то, что оно – металл). Эта особенность импликации обусловливает два правила условно-категорического силлогизма:

1. Утверждать можно только от основания к следствию, т. е. во второй посылке утверждающего модуса должно утверждаться основание импликации (первой посылки), а в выводе – ее следствие. В противном случае из двух истинных посылок может вытекать ложный вывод. Например:

Если слово стоит в начале предложения, то оно всегда пишется с большой буквы.

Слово «Москва» всегда пишется с большой буквы.

=> Слово «Москва» всегда стоит в начале предложения.

Во второй посылке утверждалось следствие, а в выводе – основание. Это утверждение от следствия к основанию и является причиной ложного вывода при истинных посылках.

2. Отрицать можно только от следствия к основанию, т. е. во второй посылке отрицающего модуса должно отрицаться следствие импликации (первой посылки), а в выводе – ее основание. В противном случае из двух истинных посылок может вытекать ложный вывод. Например:

Если слово стоит в начале предложения, то его надо писать с большой буквы.

В данном предложении слово «Москва» не стоит в начале.

=> В данном предложении слово «Москва» не надо писать с большой буквы.

Во второй посылке отрицается основание, а в выводе – следствие. Это отрицание от основания к следствию и является причиной ложного вывода при истинных посылках.

Приведем еще несколько примеров условно-категорического силлогизма – как правильных, так и с нарушениями рассмотренных правил.

Если животное является млекопитающим, то оно позвоночное.

Рептилии не являются млекопитающими.

=> Рептилии не являются позвоночными.

(Ошибка – отрицание от основания к следствию).

Если человек льстит, то он лжет.

Этот человек льстит.

=> Этот человек лжет.

(Правильное умозаключение).

Если геометрическая фигура является квадратом, то у нее все стороны равны.

Равносторонний треугольник не является квадратом.

=> У равностороннего треугольника стороны не равны.

(Ошибка – отрицание от основания к следствию).

Если металл – свинец, то он тяжелее воды.

Данный металл тяжелее воды.

=> Данный металл – свинец.

(Ошибка – утверждение от следствия к основанию).

Если небесное тело является планетой Солнечной системы, то оно движется вокруг Солнца.

Комета Галлея движется вокруг Солнца.

=> Комета Галлея является планетой Солнечной системы.

(Ошибка – утверждение от следствия к основанию).

Если вода превращается в лед, то она увеличивается в объеме.

Вода в этом сосуде превратилась в лед.

=> Вода в этом сосуде увеличилась в объеме.

(Правильное умозаключение).

Если человек является судьей, то он имеет высшее юридическое образование.

Не всякий выпускник юридического факультета МГУ является судьей.

=> Не всякий выпускник юридического факультета МГУ имеет высшее юридическое образование.

(Ошибка – отрицание от основания к следствию).

Если прямые параллельны, то у них нет общих точек.

У перекрещивающихся прямых нет общих точек.

=> Перекрещивающиеся прямые являются параллельными.

(Ошибка – утверждение от следствия к основанию).

Если техническое изделие снабжено электрическим двигателем, то оно потребляет электроэнергию.

Все изделия электронной техники потребляют электроэнергию.

=> Все изделия электронной техники снабжены электрическими двигателями.

(Ошибка – утверждение от следствия к основанию).

Вспомним, что среди сложных суждений помимо импликации (а => b) есть также эквиваленция (а <=> b). Если в импликации всегда выделяется основание и следствие, то в эквиваленции нет ни того, ни другого, так как она представляет собой сложное суждение, обе части которого тождественны (эквивалентны) друг другу. Силлогизм называется эквивалентно-категорическим, если первой посылкой силлогизма является не импликация, а эквиваленция. Например:

Если число четное, то оно делится без остатка на 2.

Число 16 – четное.

=> Число 16 делится без остатка на 2.

Поскольку в первой посылке эквивалентно-категорического силлогизма нельзя выделить ни основания, ни следствия, то рассмотренные выше правила условно-категорического силлогизма к нему неприменимы (в эквивалентно-категорическом силлогизме и утверждать, и отрицать можно как угодно).

Итак, если одна из посылок силлогизма является условным, или импликативным, суждением, а вторая – категорическим, или простым, то перед нами условно-категорический силлогизм (также часто называемый условно-категорическим умозаключением). Если же обе посылки представляют собой условные суждения, то это чисто условный силлогизм, или чисто условное умозаключение. Например:

Если вещество является металлом, то оно электропроводно.

Если вещество электропроводно, то его невозможно использовать в качестве изолятора.

=> Если вещество является металлом, то его невозможно использовать в качестве изолятора.

В данном случае не только обе посылки, но и вывод силлогизма являются условными (импликативными) суждениями. Другая разновидность чисто условного силлогизма:

Если треугольник является прямоугольным, то его площадь равна половине произведения его основания на высоту.

Если треугольник не является прямоугольным, то его площадь равна половине произведения его основания на высоту.

=> Площадь треугольника равна половине произведения его основания на высоту.

Как видим, в этой разновидности чисто условного силлогизма обе посылки являются импликативными суждениями, но вывод (в отличие от первой рассмотренной разновидности) представляет собой простое суждение.

Кроме разделительно-категорических и условно-категорических умозаключений, или силлогизмов, существуют также условно-разделительные умозаключения. В условно-разделительном умозаключении (силлогизме) первая посылка является условным, или импликативным суждением, а вторая посылка – это разделительное, или дизъюнктивное, суждение. Важно отметить, что в условном (импликативном) суждении может быть не одно основание и одно следствие (как в тех примерах, которые мы рассматривали до сих пор), а больше оснований или следствий. Например, в суждении Если поступать в МГУ, то надо много заниматься или же надо иметь много денег из одного основания вытекает два следствия. В суждении Если поступать в МГУ, то надо много заниматься, а если поступать в МГИМО, то тоже надо много заниматься из двух оснований вытекает одно следствие. В суждении Если страной правит мудрый человек, то она процветает, а если ею управляет проходимец, то она бедствует из двух оснований вытекают два следствия. В суждении Если я выступлю против окружающей меня несправедливости, то останусь человеком, хотя жестоко пострадаю; если равнодушно пройду мимо нее, то перестану себя уважать, хотя и буду цел и невредим; а если стану всячески содействовать ей, то превращусь в животное, хотя и достигну материального и карьерного благополучия из трех оснований вытекает три следствия.

Если в первой посылке условно-разделительного силлогизма содержится два основания или следствия, то такой силлогизм называется дилеммой, если оснований или следствий три, то он называется трилеммой, а если первая посылка включает в себя более трех оснований или следствий, то силлогизм является полилеммой. Чаще всего в мышлении и речи встречается дилемма, на примере которой мы и рассмотрим условно-разделительный силлогизм (также часто называемый условно-разделительным умозаключением).

Дилемма может быть конструктивной (утверждающей) и деструктивной (отрицающей). Каждый из этих видов дилеммы в свою очередь делится на две разновидности: как конструктивная, так и деструктивная дилемма может быть простой или сложной.

В простой конструктивной дилемме из двух оснований вытекает одно следствие, вторая посылка представляет собой дизъюнкцию оснований, а в выводе утверждается это одно следствие в виде простого суждения. Например:

Если поступать в МГУ, то надо много заниматься, а если поступать в МГИМО, то тоже надо много заниматься.

Можно поступать в МГУ или МГИМО.

=> Надо много заниматься.

В первой посылке сложной конструктивной дилеммы из двух оснований вытекают два следствия, вторая посылка представляет собой дизъюнкцию оснований, а вывод является сложным суждением в виде дизъюнкции следствий. Например:

Если страной правит мудрый человек, то она процветает, а если ею управляет проходимец, то она бедствует.

Страной может управлять мудрый человек или проходимец.

=> Страна может процветать или бедствовать.

В первой посылке простой деструктивной дилеммы из одного основания вытекают два следствия, вторая посылка представляет собой дизъюнкцию отрицаний следствий, а в выводе отрицается основание (происходит отрицание простого суждения). Например:

Если поступать в МГУ, то надо много заниматься или же надо много денег.

Я не хочу много заниматься или же тратить много денег.

=> Я не буду поступать в МГУ.

В первой посылке сложной деструктивной дилеммы из двух оснований вытекают два следствия, вторая посылка представляет собой дизъюнкцию отрицаний следствий, а вывод является сложным суждением в виде дизъюнкции отрицаний оснований. Например:

Если философ считает первоначалом мира материю, то он материалист, а если он считает первоначалом мира сознание, то он идеалист.

Этот философ не материалист или не идеалист.

=> Этот философ не считает первоначалом мира материю, или он не считает первоначалом мира сознание.

Поскольку первая посылка условно-разделительного силлогизма является импликацией, а вторая – дизъюнкцией, его правила – те же самые, что и рассмотренные выше правила условно-категорического и разделительно-категорического силлогизмов.

Приведем еще несколько примеров дилеммы.

Если изучать английский, то необходима каждодневная разговорная практика, а если изучать немецкий, то также необходима каждодневная разговорная практика.

Можно изучать английский или немецкий.

=> Необходима каждодневная разговорная практика.

(Простая конструктивная дилемма).

Если я признаюсь в совершенном проступке, то понесу заслуженное наказание, а если я попытаюсь скрыть его, то буду испытывать угрызения совести.

Я или признаюсь в совершенном проступке, или попытаюсь скрыть его.

=> Я понесу заслуженное наказание или буду испытывать угрызения совести.

(Сложная конструктивная дилемма).

Если он женится на ней, то потерпит полный крах или же будет влачить жалкое существование.

Он не хочет потерпеть полный крах или же влачить жалкое существование.

=> Он не женится на ней.

(Простая деструктивная дилемма).

Если скорость Земли при ее движении по орбите была бы больше 42 км/с, то она покинула бы Солнечную систему; а если ее скорость была бы меньше 3 км/с, то она «упала» бы на Солнце.

Земля не покидает Солнечную систему и не «падает» на Солнце.

=> Скорость Земли при ее движении по орбите не больше 42 км/с и не меньше 3 км/с.

(Сложная деструктивная дилемма).

В индукции из нескольких частных случаев выводится общее правило, рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, как правило, вероятностны. Индукция бывает полной и неполной. В полной индукции перечисляются все объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются все девять крупных планет Солнечной системы, то такая индукция является полной:

Меркурий движется.

Венера движется.

Земля движется.

Марс движется.

…

Плутон движется.

Меркурий, Венера, Земля, Марс, Плутон – это крупные планеты Солнечной системы.

=> Все крупные планеты Солнечной системы движутся.

В неполной индукции перечисляются некоторые объекты из какой-либо группы и делается вывод обо всей этой группе. Например, если в посылках индуктивного умозаключения перечисляются не все девять крупных планет Солнечной системы, а только три из них, то такая индукция является неполной:

Меркурий движется.

Венера движется.

Земля движется.

Меркурий, Венера, Земля – это крупные планеты Солнечной системы.

=> Все крупные планеты Солнечной системы движутся.

Понятно, что выводы полной индукции достоверны, а неполной – вероятностны, однако полная индукция встречается редко, и поэтому под индуктивными умозаключениями обычно подразумевается неполная индукция.

Чтобы повысить степень вероятности выводов неполной индукции, следует соблюдать следующие важные правила.

1. Необходимо подбирать как можно больше исходных посылок. Для примера рассмотрим следующую ситуацию. Требуется проверить уровень успеваемости учащихся в некоей школе. Предположим, что в ней учится 1000 человек. По методу полной индукции надо протестировать на предмет успеваемости каждого ученика из этой тысячи. Поскольку сделать это довольно сложно, можно использовать метод неполной индукции: протестировать какую-то часть учащихся и сделать общий вывод об уровне успеваемости в данной школе. Различные социологические опросы также базируются на применении неполной индукции. Очевидно, что чем большее число учеников подвергнется тестированию, тем более надежной будет база для индуктивного обобщения и более точным получится вывод. Однако просто большего числа исходных посылок, как того требует рассматриваемое правило, для повышения степени вероятности индуктивного обобщения недостаточно. Допустим, тестирование пройдет немалое число учащихся, но, волей случая, среди них окажутся одни только неуспевающие. В этой ситуации мы придем к ложному индуктивному выводу о том, что уровень успеваемости в данной школе очень низок. Поэтому первое правило дополняется вторым.

2. Необходимо подбирать разнообразные посылки.

Возвращаясь к нашему примеру, отметим, что множество тестируемых должно быть не просто по возможности большим, но и специально (по какой-то системе) сформированным, а не случайно подобранным, т. е. надо позаботиться о том, чтобы в него вошли учащиеся (примерно в одинаковом количественном отношении) из разных классов, параллелей и т. п.

3. Необходимо делать вывод только на основе существенных признаков. Если, допустим, во время тестирования выясняется, что ученик 10 класса не знает наизусть всю Периодическую систему химических элементов, то этот факт (признак) является несущественным для вывода о его успеваемости. Однако если тестирование показывает, что ученик 10 класса частицу НЕ с глаголом пишет слитно, то этот факт (признак) следует признать существенным (важным) для вывода об уровне его образованности и успеваемости.

Таковы основные правила неполной индукции. Теперь обратимся к ее наиболее распространенным ошибкам. Говоря о дедуктивных умозаключениях, мы рассматривали ту или иную ошибку вместе с правилом, нарушение которого ее порождает. В данном случае сначала представлены правила неполной индукции, а потом, отдельно, – ее ошибки. Это объясняется тем, что каждая из них не связана непосредственно с каким-то из вышеприведенных правил. Любую индуктивную ошибку можно рассматривать как результат одновременного нарушения всех правил, и в то же время нарушение каждого правила можно представить как причину, приводящую к любой из ошибок.

Первая ошибка, часто встречающаяся в неполной индукции, называется поспешным обобщением. Скорее всего, каждый из нас хорошо с ней знаком. Всем приходилось слышать такие высказывания, как Все мужчины черствые, Все женщины легкомысленные, и т. п. Эти расхожие стереотипные фразы представляют собой не что иное, как поспешное обобщение в неполной индукции: если некоторые объекты из какой-либо группы обладают неким признаком, то это вовсе не означает, что данным признаком характеризуется вся группа без исключения. Из истинных посылок индуктивного умозаключения может вытекать ложный вывод, если допустить поспешное обобщение. Например:

К. учится плохо.

Н. учится плохо.

С. учится плохо.

К., Н., С. – это ученики 10 «А».

=> Все ученики 10 «А» учатся плохо.

Неудивительно, что поспешное обобщение лежит в основе многих голословных утверждений, слухов и сплетен.

Вторая ошибка носит длинное и на первый взгляд странное название: после этого, значит, по причине этого (с лат. post hoc, ergo propter hoc). В данном случае речь идет о том, что если одно событие происходит после другого, то это не означает с необходимостью их причинно-следственную связь. Два события могут быть связаны всего лишь временной последовательностью (одно – раньше, другое – позже). Когда мы говорим, что одно событие обязательно является причиной другого, потому что одно из них произошло раньше другого, то допускаем логическую ошибку. Например, в следующем индуктивном умозаключении обобщающий вывод является ложным, несмотря на истинность посылок:

Позавчера двоечнику Н. перебежала дорогу черная кошка, и он получил двойку.

Вчера двоечнику Н. перебежала дорогу черная кошка, и его родителей вызвали в школу.

Сегодня двоечнику Н. перебежала дорогу черная кошка, и его исключили из школы.

=> Во всех несчастьях двоечника Н. виновата черная кошка.

Неудивительно, что эта распространенная ошибка породила множество небылиц, суеверий и мистификаций.

Третья ошибка, широко распространенная в неполной индукции, называется подмена условного безусловным. Рассмотрим индуктивное умозаключение, в котором из истинных посылок вытекает ложный вывод:

Дома вода кипит при температуре 100 °C.

На улице вода кипит при температуре 100 °C.

В лаборатории вода кипит при температуре 100 °C.

=> Вода везде кипит при температуре 100 °C.

Мы знаем, что высоко в горах вода кипит при более низкой температуре. На Марсе температура кипящей воды была бы равна примерно 45 °C. Так что вопрос Всегда ли и везде ли кипяток горяч? не является нелепым, как это может показаться на первый взгляд. И ответ на этот вопрос будет: Не всегда и не везде. То, что проявляется в одних условиях, может не проявляться в других. В посылках рассмотренного примера присутствует условное (происходящее в определенных условиях), которое подменяется безусловным (происходящим во всех условиях одинаково, не зависящим от них) в выводе.

Хороший пример подмены условного безусловным содержится в известной нам с детства сказке про вершки и корешки, в которой речь идет о том, как мужик и медведь посадили репу, договорившись поделить урожай следующим образом: мужику – корешки, медведю – вершки. Получив ботву от репы, медведь понял, что мужик его обманул, и совершил логическую ошибку подмены условного безусловным – решил, что надо всегда брать только корешки. Поэтому на следующий год, когда пришло время делить урожай пшеницы, медведь отдал мужику вершки, а себе снова взял вершки – и опять остался ни с чем.

Приведем еще несколько примеров ошибок в индуктивных умозаключениях.

1. Как известно, дед, бабка, внучка, Жучка, кошка и мышка вытащили репку. Однако дед репку не вытащил, бабка тоже ее не вытащила. Внучка, Жучка и кошка также не вытащили репку. Ее удалось вытащить только после того, как на помощь пришла мышка. Следовательно, репку вытащила мышка.

(Ошибка – «после этого», значит «по причине этого»).

2. Долгое время в математике считалось, что все уравнения можно решить в радикалах. Этот вывод был сделан на том основании, что исследованные уравнения первой, второй, третьей и четвертой степеней возможно привести к виду х_n = а. Однако впоследствии оказалось, что уравнения пятой степени нельзя решить в радикалах.

(Ошибка – поспешное обобщение).

3. В классическом, или ньютоновском, естествознании считалось, что пространство и время неизменны. Это убеждение основывалось на том, что, где бы ни находились различные материальные объекты и что бы с ними ни происходило, время для каждого из них течет одинаково и пространство остается одним и тем же. Однако появившаяся в начале XX века теория относительности показала, что пространство и время вовсе не неизменны. Так, например, при движении материальных объектов со скоростями, близкими к скорости света (300 000 км/с), время для них значительно замедляется, а пространство искривляется, перестает быть евклидовым.

(Ошибка классического представления о пространстве и времени – подмена условного безусловным).

Неполная индукция бывает популярной и научной. В популярной индукции вывод делается на основе наблюдения и простого перечисления фактов, без знания их причины, а в научной индукции вывод делается не только на основе наблюдения и перечисления фактов, но еще и на основе знания их причины. Поэтому научная индукция (в отличие от популярной) характеризуется намного более точными, почти достоверными выводами.

Например, первобытные люди видят, как солнце каждый день встает на востоке, медленно движется в течение дня по небу и закатывается на западе, но они не знают, почему так происходит, им неизвестна причина этого постоянно наблюдаемого явления. Понятно, что они могут сделать умозаключение, используя только популярную индукцию и рассуждая примерно следующим образом: Позавчера солнце взошло на востоке, вчера солнце взошло на востоке, сегодня солнце взошло на востоке, следовательно, солнце всегда всходит на востоке. Мы, как и первобытные люди, наблюдаем каждодневный восход солнца на востоке, но в отличие от них знаем причину этого явления: Земля вращается вокруг своей оси в одном и том же направлении с неизменной скоростью, в силу чего Солнце появляется каждое утро в восточной стороне неба. Поэтому то умозаключение, которое делаем мы, представляет собой научную индукцию и выглядит примерно так: Позавчера Солнце взошло на востоке, вчера Солнце взошло на востоке, сегодня Солнце взошло на востоке; причем это происходит оттого, что уже несколько миллиардов лет Земля вращается вокруг своей оси и будет вращаться так же и дальше в течение многих миллиардов лет, находясь на одном и том же расстоянии от Солнца, которое родилось раньше Земли и будет существовать дольше нее; следовательно, для земного наблюдателя Солнце всегда всходило и будет всходить на востоке.

Главное отличие научной индукции от популярной заключается в знании причин происходящих событий. Поэтому одна из важных задач не только научного, но и повседневного мышления – это обнаружение причинных связей и зависимостей в окружающем нас мире.

В логике рассматриваются четыре метода установления причинных связей. Впервые их выдвинул английский философ XVII века Фрэнсис Бэкон, а всесторонне разработаны они были в XIX веке – английским логиком и философом Джоном Стюартом Миллем.

Метод единственного сходства строится по следующей схеме:

При условиях ABC возникает явление х.

При условиях ADE возникает явление х.

При условиях AFG возникает явление х.

=> Вероятно, условие А – это причина явления х.

Перед нами – три ситуации, в которых действуют условия А, В, С, D, Е, F, G, причем одно из них (A) повторяется в каждой. Это повторяющееся условие – единственное, в чем схожи между собой данные ситуации. Далее надо обратить внимание на то, что во всех ситуациях возникает явление х. Из этого можно сделать вероятный вывод, что условие А представляет собой причину явления х (одно из условий все время повторяется, и явление при этом постоянно возникает, что и дает основание объединить первое и второе причинно-следственной связью). Например, требуется установить, какой продукт питания вызывает у человека аллергию. Допустим, в течение трех дней аллергическая реакция неизменно возникала. При этом в первый день человек употреблял в пищу продукты А, В, С, во второй день – продукты A, D, Е, в третий день – продукты А, Е, G, т. е. на протяжении трех дней повторно принимался в пищу только продукт А, который скорее всего и является причиной аллергии.

Продемонстрируем метод единственного сходства на примерах.

1. Объясняя структуру условного (импликативного) суждения, преподаватель привел три примера различного содержания:

• Если по проводнику проходит электрический ток, то проводник нагревается;

• Если слово стоит в начале предложения, то его надо писать с большой буквы;

• Если взлетная полоса покрыта льдом, то самолеты не могут взлететь.

2. Анализируя примеры, он обратил внимание студентов на один и тот же союз ЕСЛИ… ТО, соединяющий простые суждения в сложное, и сделал вывод о том, что это обстоятельство дает основание все три сложных суждения записать одинаковой формулой.

3. Однажды Е. Ф. Буринский налил на старое ненужное письмо красные чернила и сфотографировал его через красное стекло. Проявляя фотопластинку, он не подозревал, что делает удивительное открытие. На негативе пятно исчезло, но проступил текст, залитый чернилами. Последующие опыты с разными по цвету чернилами привели к тому же результату – текст выявлялся. Следовательно, причиной проявления текста является его фотографирование через красное стекло. Буринский первым стал применять свой метод фотографирования в криминалистике.

Метод единственного различия строится таким образом:

При условиях A BCD возникает явление х.

При условиях BCD не возникает явление х.

=> Вероятно, условие А – это причина явления х.

Как видим, две ситуации различаются между собой только в одном: в первой условие А присутствует, а во второй оно отсутствует. Причем в первой ситуации явление х возникает, а во второй – не возникает. На основании этого можно предположить, что условие А и есть причина явления х. Например, в воздушной среде металлический шарик падает на землю раньше, чем перышко, брошенное одновременно с ним с той же высоты, т. е. шарик движется к земле с большим ускорением, чем перышко. Однако если проделать данный эксперимент в безвоздушной среде (все условия – те же самые, кроме наличия воздуха), то и шарик, и перышко будут падать на землю одновременно, т. е. с одинаковым ускорением. Видя, что в воздушной среде различное ускорение падающих тел имеет место, а в безвоздушной – не имеет, можно заключить, что, по всей вероятности, сопротивление воздуха является причиной падения разных тел с различным ускорением.

Примеры применения метода единственного различия приведены ниже.

1. Листья растения, выросшего в подвале, не имеют зеленой окраски. Листья того же растения, выросшего в обычных условиях, являются зелеными. В подвале нет света. В обычных условиях растение произрастает на солнечном свету. Следовательно, он является причиной возникновения зеленого цвета растений.

2. Климат Японии является субтропическим. В лежащем почти на тех же широтах недалеко от Японии Приморье климат намного более суров. У берегов Японии проходит теплое течение. У берегов Приморья теплого течения нет. Следовательно, причина различия в климате Приморья и Японии заключается во влиянии морских течений.

Метод сопутствующих изменений построен так:

При условиях A₁BCD возникает явление х₁.

При условиях A₂BCD возникает явление х₂.

При условиях A₃BCD возникает явление х₃.

=> Вероятно, условие А – это причина явления х.

Изменение одного из условий (при неизменности прочих условий) сопровождается изменением происходящего явления, в силу чего можно утверждать, что данное условие и указанное явление объединены причинно-следственной связью. Например, при увеличении скорости движения в два раза пройденный путь увеличивается также вдвое; если скорость возрастает в три раза, то и пройденное расстояние становится в три раза большим. Следовательно, увеличение скорости является причиной увеличения пройденного пути (разумеется, за один и тот же промежуток времени).

Продемонстрируем метод сопутствующих изменений на примерах.

1. Еще в древности было замечено, что периодичность морских приливов и изменение их высоты соответствуют изменениям в положении Луны. Наибольшие приливы приходятся на дни новолуний и полнолуний, наименьшие – на так называемые дни квадратур (когда направления от Земли к Луне и Солнцу образуют прямой угол). На основании этих наблюдений был сделан вывод о том, что морские приливы обусловливаются действием Луны.

2. Всякий, кто сжимал в руках мяч, знает, что если увеличить внешнее давление на него, то мяч уменьшится. Если же прекратить это давление, то мяч возвращается к своим прежним размерам. Французский ученый XVII века Блез Паскаль, видимо, первым обнаружил данное явление, причем он сделал это весьма своеобразным и достаточно убедительным образом. Отправляясь со своими помощниками в гору, он захватил с собой не только барометр, но и пузырь, частично надутый воздухом. Паскаль заметил, что объем пузыря увеличивался по мере подъема, а на обратном пути стал уменьшаться. Когда же исследователи достигли подножия горы, пузырь принял первоначальные размеры. Из этого был сделан вывод о том, что высота горного подъема прямо пропорциональна изменению внешнего давления, т. е. находится с ним в причинно-следственной связи.

Метод остатков строится следующим образом:

При условиях ABC возникает явление xyz.

Известно, что часть у из явления xyz вызывается условием В.

Известно, что часть z из явления xyz вызывается условием С.

=> Вероятно, условие А – это причина явления X.

В данном случае происходящее явление разбито на составные части и известна причинная связь каждой из них, кроме одной, с каким-либо условием. Если остается только одна часть из возникающего явления и только одно условие из совокупности условий, порождающих это явление, то можно утверждать, что оставшееся условие представляет собой причину оставшейся части рассмотренного явления. Например, рукопись автора читали редакторы А, В, С, делая в ней пометки шариковыми авторучками. Причем известно, что редактор В правил рукопись синими чернилами (у), а редактор С – красными (z). Однако в рукописи имеются пометки, сделанные зелеными чернилами (х). Можно заключить, что, скорее всего, они оставлены редактором А.

Примеры применения метода остатков приведены ниже.

1. Наблюдая за движением планеты Уран, астрономы XIX века заметили, что она несколько отклоняется от своей орбиты. Было установлено, что Уран отклоняется на величины а, b, с, причем эти отклонения вызваны влиянием соседних планет А, В, С. Однако также было замечено, что Уран в своем движении отклоняется не только на величины а, b, с, но еще и на величину d. Из этого сделали предположительный вывод о наличии за орбитой Урана пока неизвестной планеты, которая вызывает данное отклонение. Французский ученый Леверье рассчитал положение этой планеты, а немецкий ученый Галле с помощью сконструированного им телескопа нашел ее на небесной сфере. Так в XIX веке была открыта планета Нептун.

2. Известно, что дельфины могут с большой скоростью передвигаться в воде. Расчеты показали, что их мускульная сила, даже при совершенно обтекаемой форме тела, не в состоянии обеспечить столь высокую скорость. Предположили, что часть причины заключается в особом строении кожи дельфинов, срывающей завихрения воды. В дальнейшем это предположение было подтверждено экспериментально.

В умозаключениях по аналогии на основе сходства предметов в одних признаках делается вывод об их сходстве и в других признаках. Структура аналогии может быть представлена следующей схемой:

Предмет А имеет признаки а, b, с, d.

Предмет В имеет признаки а, b, с.

=> Вероятно, предмет В имеет признак d.

В данной схеме А и В – это сравниваемые или уподобляемые друг другу предметы (объекты); а, b, с – сходные признаки; d – это переносимый признак. Рассмотрим пример умозаключения по аналогии:

Сочинения философа Секста Эмпирика, выпущенные издательством «Мысль» в серии «Философское наследие», снабжены вступительной статьей, комментариями и предметно-именным указателем.

В аннотации к книжной новинке – сочинениям философа Фрэнсиса Бэкона – говорится, что они выпущены издательством «Мысль» в серии «Философское наследие» и снабжены вступительной статьей и комментариями.

=> Скорее всего, выпущенные сочинения Фрэнсиса Бэкона так же, как и сочинения Секста Эмпирика, снабжены предметно-именным указателем.

В данном случае сравниваются (сопоставляются) два объекта: ранее изданные сочинения Секста Эмпирика и выходящие в свет сочинения Фрэнсиса Бэкона. Сходные признаки этих двух книг состоят в том, что они выпускаются одним и тем же издательством, в одной и той же серии, снабжены вступительными статьями и комментариями. На основании этого с большой степенью вероятности можно утверждать, что если сочинения Секста Эмпирика снабжены предметно-именным указателем, то им будут снабжены и сочинения Фрэнсиса Бэкона. Таким образом, наличие предметно-именного указателя является переносимым признаком в рассмотренном примере.

Умозаключения по аналогии делятся на два вида: аналогия свойств и аналогия отношений.

В аналогии свойств сравниваются два предмета, а переносимым признаком является какое-либо свойство этих предметов. Приведенный выше пример представляет собой аналогию свойств.

Приведем еще несколько примеров.

1. Жабры для рыб – это то же самое, что легкие для млекопитающих.

2. Повесть А. Конан Дойла «Знак четырех» о приключениях благородного сыщика Шерлока Холмса, отличающаяся динамичным сюжетом, мне очень понравилась. Я не читал повесть А. Конан Дойла «Собака Баскервиллей», но знаю, что она посвящена приключениям благородного сыщика Шерлока Холмса и отличается динамичным сюжетом. Скорее всего, эта повесть мне также очень понравится.

3. На Всесоюзном съезде физиологов в Ереване (1964 г.) московские ученые М. М. Бонгард и А. Л. Вызов продемонстрировали установку, которая моделировала цветовое зрение человека. При быстром включении ламп она безошибочно распознавала цвет и его интенсивность. Интересно, что эта установка имела ряд тех же самых недостатков, что и зрение человека.

Например, оранжевый свет после интенсивного красного в первое мгновение воспринимался ей как синий или зеленый.

В аналогии отношений сравниваются две группы предметов, а переносимым признаком является какое-либо отношение между предметами внутри этих групп. Пример аналогии отношений:

В математической дроби числитель и знаменатель находятся в обратном отношении: чем больше знаменатель, тем меньше числитель.

Человека можно сравнить с математической дробью: числитель ее – это то, что он собой представляет на самом деле, а знаменатель – то, что он о себе думает, как себя оценивает.

=> Вероятно, что чем выше человек себя оценивает, тем хуже он становится на самом деле.

Как видим, сравниваются две группы объектов. Одна – это числитель и знаменатель в математической дроби, а другая – реальный человек и его самооценка. Причем отношение обратной зависимости между объектами переносится из первой группы во вторую.

Приведем еще два примера.

1. Сущность планетарной модели атома Э. Резерфорда состоит в том, что в нем вокруг положительно заряженного ядра по разным орбитам движутся отрицательно заряженные электроны; так же, как и в Солнечной системе, планеты движутся по разным орбитам вокруг единого центра – Солнца.

2. Два физических тела (по закону всемирного тяготения Ньютона) притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними; так же и два неподвижных друг относительно друга точечных заряда (по закону Кулона) взаимодействуют с электростатической силой, прямо пропорциональной произведению зарядов и обратно пропорциональной квадрату расстояния между ними.

В силу вероятностного характера своих выводов аналогия, конечно же, более близка к индукции, чем к дедукции. Поэтому неудивительно, что основные правила аналогии, соблюдение которых позволяет повысить степень вероятности ее выводов, во многом напоминают уже известные нам правила неполной индукции.

Во-первых, необходимо делать вывод на основе возможно большего количества сходных признаков уподобляемых предметов.

Во-вторых, эти признаки должны быть разнообразными.

В-третьих, сходные признаки должны являться существенными для сравниваемых предметов.

В-четвертых, должна присутствовать необходимая (закономерная) связь между сходными признаками и переносимым признаком.

Первые три правила аналогии фактически повторяют правила неполной индукции. Пожалуй, наиболее важным является четвертое правило, о связи сходных признаков и переносимого признака. Вернемся к примеру аналогии, рассмотренному в начале данного параграфа. Переносимый признак – наличие предметно-именного указателя в книге – тесно связан со сходными признаками – издательство, серия, вступительная статья, комментарии (книги такого жанра обязательно снабжаются предметно-именным указателем). Если переносимый признак (например, объем книги) не связан закономерно со сходными признаками, то вывод умозаключения по аналогии может получиться ложным:

Сочинения философа Секста Эмпирика, выпущенные издательством «Мысль» в серии «Философское наследие», снабжены вступительной статьей, комментариями и имеют объем в 590 страниц.

В аннотации к книжной новинке – сочинениям философа Фрэнсиса Бэкона – говорится, что они выпущены издательством «Мысль» в серии «Философское наследие» и снабжены вступительной статьей и комментариями.

=> Скорее всего, выпущенные сочинения Фрэнсиса Бэкона, как и сочинения Секста Эмпирика, имеют объем в 590 страниц.

Несмотря на вероятностный характер выводов, умозаключения по аналогии имеют немало достоинств. Аналогия представляет собой хорошее средство иллюстрации и разъяснения какого-либо сложного материала, является способом придания ему художественной образности, часто наводит на научные и технические открытия. Так, на основе аналогии отношений построены многие выводы в бионике – науке, которая занимается изучением объектов и процессов живой природы для создания различных технических приспособлений. Например, построены машины-снегоходы, принцип передвижения которых заимствован у пингвинов. Используя особенность восприятия медузой инфразвука с частотой 8—13 колебаний в секунду (что позволяет ей заранее распознавать приближение бури по штормовым инфразвукам), ученые создали электронный аппарат, способный предсказывать наступление шторма за 15 часов. Изучая полет летучей мыши, которая испускает ультразвуковые колебания и затем улавливает их отражение от предметов, тем самым безошибочно ориентируясь в темноте, человек сконструировал радиолокаторы, обнаруживающие различные объекты и точно определяющие место их расположения независимо от погодных условий.

Как видим, умозаключения по аналогии достаточно широко используются как в повседневном, так и в научном мышлении.