8. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА

В 1904 году Лоренц предложил формулы для преобразования координат, которые обеспечивают инвариантность уравнений Максвелла при переходе от одной инерциальной системы отсчета к другой: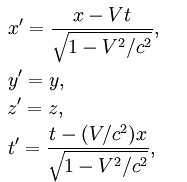


где с – скорость света в вакууме.

Формулы были названы Пуанкаре преобразованиями Лоренца.

Инвариантным относительно преобразований Лоренца является так называемый пространственно-временной интервал, или просто интервал. Пусть события произошли в точке х1, у1, z1 в момент времени t1 и в точке х2, у2, z2 в момент времени t2. Интервалом между событиями, или, как говорят, интервалом между точками х1, у1, z1, t1 и х2, у2, z2, t2, называется величина s, квадрат которой определяется формулой

S2 = С2 (t2 – t1)2 – (Х2 – Х1)2 – (У2 – У1)2 – (Z2 – Z1)2. (1)

В подвижной системе отсчета квадрат интервала S записывается в виде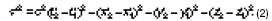


Подставляя формулу (1) в (2), убедимся, что s2 = s'2 = inv. Впервые понятие интервала ввел Пуанкаре, и он же показал, что интервал является инвариантом при преобразованиях Лоренца.

Из преобразований Лоренца следует сокращение длины движущегося стержня, а именно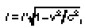где l = x2 – x1 и l' = x'2 – x1, и замедление хода движущихся часов, а именно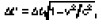, где ?t = t2– t1 и  ?t' = = t'2-t' 1.